Abstract's details
Slope Correction for Ocean Radar Altimetry
Event: 2014 Ocean Surface Topography Science Team Meeting
Session: The Geoid, Mean Sea Surfaces and Mean Dynamic Topography
Presentation type: Oral
Thanks to recent improvements from CryoSat and the Jason-1 Geodetic Mission, the slope of the geoid is now known to about 2 micro-radians. Further improvement in mean sea surface (MSS), mean dynamic topography, and gravity field mapping now requires a correction for slope error, which until now has been ignored. Without this correction there will be geographically fixed errors as large as 50 mm in sea level and 0.5 m/s in inferred geostrophic velocity.
An altimeter ranges to a patch of surface area known as the footprint. If the median surface in the footprint lies parallel to the ellipsoid, then the footprint center will be at nadir and no correction to range is required. However, if the median surface is inclined to the ellipsoid by an angle, S, then the measured range is less than the range to median sea level at nadir by an amount S-squared times H_effective / 2, where H_effective = H / (1 + H/R), H being orbital altitude and R being the local Earth radius. Because S is small, the correction can be computed assuming that H_effective is a constant for any altimeter mission. We have computed the correction at an H_effective of 1000 km. Our computation can be rescaled to 1104 km for Topex and Jason, or 703 km for AltiKa, Envisat, and ERS, and is available at ftp://topex.ucsd.edu/pub/global_VD_1min/DH.grd.
The global root-mean-square value for S is 35 micro-radians, yielding a correction of only 0.7 mm at Jason altitude. However, over a seamount or ocean trench, S can reach 300 micro-radians. In these locations the correction to sea level can be 50 mm, and the along-track gradient of the correction can be 5 micro-radians, equivalent to 0.5 m/s of geostrophic velocity in middle latitudes.
We will present a derivation and maps of the correction and its impact on inferred geostrophy. Further details can be found in the Journal of Geodesy 2014 at doi:10.1007/s00190-014-0720-1.
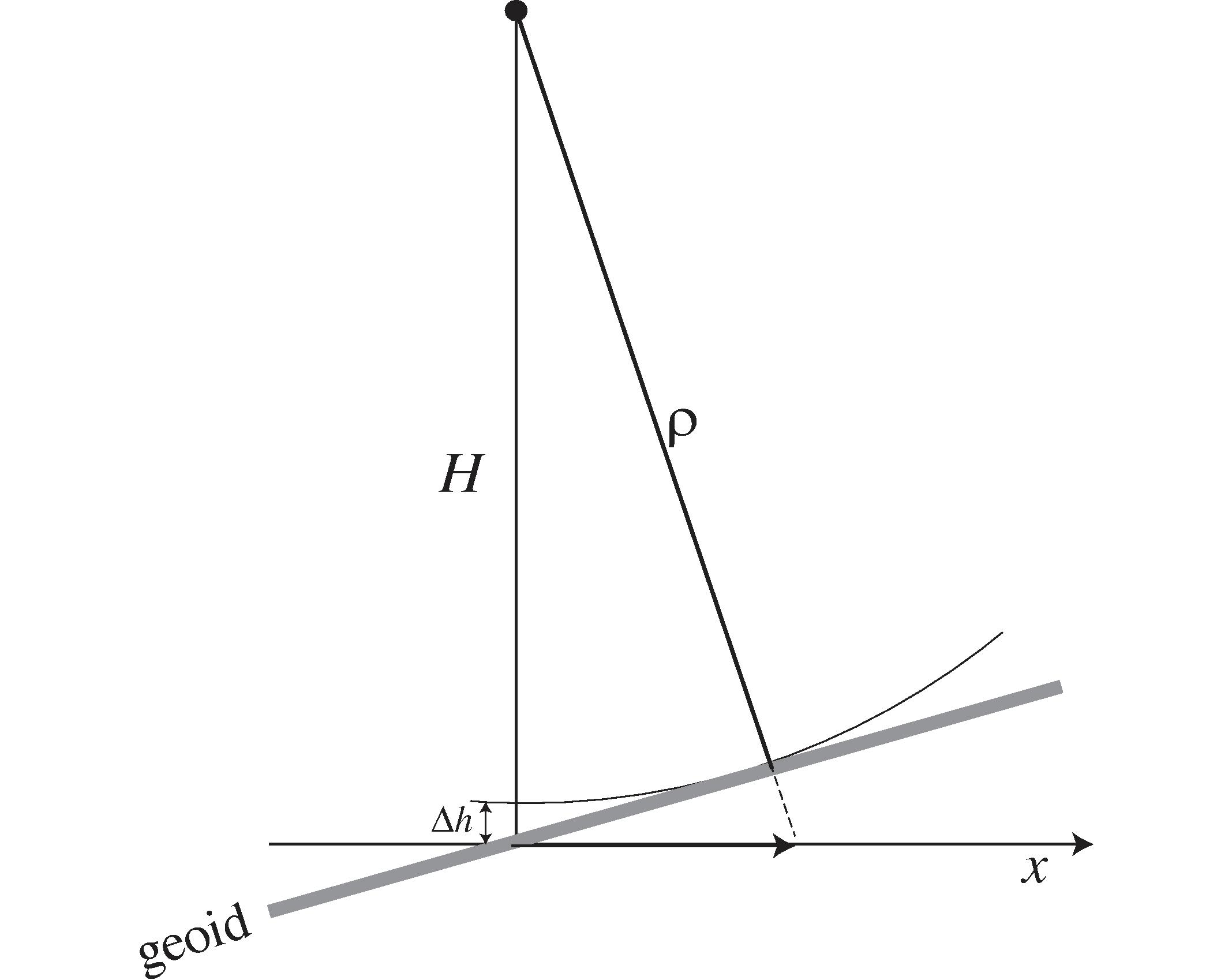
An altimeter ranges to a patch of surface area known as the footprint. If the median surface in the footprint lies parallel to the ellipsoid, then the footprint center will be at nadir and no correction to range is required. However, if the median surface is inclined to the ellipsoid by an angle, S, then the measured range is less than the range to median sea level at nadir by an amount S-squared times H_effective / 2, where H_effective = H / (1 + H/R), H being orbital altitude and R being the local Earth radius. Because S is small, the correction can be computed assuming that H_effective is a constant for any altimeter mission. We have computed the correction at an H_effective of 1000 km. Our computation can be rescaled to 1104 km for Topex and Jason, or 703 km for AltiKa, Envisat, and ERS, and is available at ftp://topex.ucsd.edu/pub/global_VD_1min/DH.grd.
The global root-mean-square value for S is 35 micro-radians, yielding a correction of only 0.7 mm at Jason altitude. However, over a seamount or ocean trench, S can reach 300 micro-radians. In these locations the correction to sea level can be 50 mm, and the along-track gradient of the correction can be 5 micro-radians, equivalent to 0.5 m/s of geostrophic velocity in middle latitudes.
We will present a derivation and maps of the correction and its impact on inferred geostrophy. Further details can be found in the Journal of Geodesy 2014 at doi:10.1007/s00190-014-0720-1.
Contribution: 30Red0900-4_OSTST2014_Smith_Sandwell_Slope_Correction_v2.pdf (pdf, 4165 ko)
Back to the list of abstract